Delay-Sensitive Cross-Layer Optimization

Cross-layer optimization refers to a resource optimization problem for wireless networks (such as OFDMA/SDMA/Relay...etc). By cross-layer design, we refer to a joint consideration of the PHY and the MAC (or other layer) in the resource allocation. This may refer to the joint consideration of PHY (such as power or data rate) and MAC parameters (such as user scheduling, random access) in the optimization variables. This may also refer to the joint consideration of PHY (throughput) and MAC (e.g. delay) performance in the optimization objective. General cross-layer optimization is an interesting and challenging problem. For instance, to capture the PHY dynamics, one has to rely on information theory and communication theory. On the other hand, to capture the delay dynamics, one has to rely on queueing theory. Integration of information theory and queueing theory is not easy and brute-force approach cannot be used to obtain useful solutions with insights. The following are some of the ongoing research focus related to cross-layer optimization.
- Discuss stability region of the queuing system under bursty arrivals and wireless fading channels.
-
-Derive control policy (function of CSI and QSI) by maximizing the Lyapunov Stability Drift - throughput optimal control (in stability sense)
-
-Asymptotically delay optimal at large delay regime
(A) Queue stability and lyapunov stablity drift

Major Approaches and the key challenges
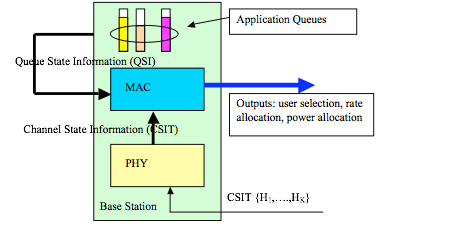
Delay-optimal control policy should be a function of both the channel state information (CSI) and queue state information (QSI). Incorporating delay consideration into wireless network optimization has always been a challenging problem. There have been various existing approaches to deal with the problem. They are:
-
-Consider symmetric homogeneous users in multi-access and broadcast channels
-
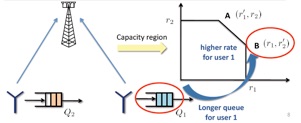
-Utilize stochastic majorization theory and polymatroid structure of the capacity region to prove that “Longest Queue Highest Possible Rate (LQHPR) policy is delay optimal.
(B) Stochastic Majorization theory for symmetric systems
-
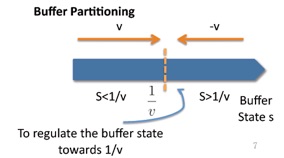
-Convert the delay constraints in the optimization problem into an equivalent “average rate constraint” using large derivation theory
-
-Solve the equivalent problem entirely in information theory domain.
-
-Derived policy is a function of CSI only (does not adapt to QSI)
-
-Good for large delay regime.
(C) Large Derivation Theory and Equivalent Rate Constraint
-
-General formulation for delay-optimal control problem in wireless networks
-
-Constructive approach to derive delay-optimal policy (function of both CSI and QSI)
-
-Good for any delay regime.
-
-Curse of dimensionality (exponentially large state space)
-
-Complex solutions and difficult to solve the Bellman’s equation in real time.
(D) Markov Decision Process (MDP) and Stochastic CONTROL

What we want to do?
The focus of the research is to investigate a systematic method for low complexity delay-optimal control solution which works for general delay regime. We have to tackle the intrinsic curse of dimensionality for heterogeneous networks (users are not statistically identical). We also would like to obtain insights on the structure of the delay-optimal policy (such as delay-optimal precoder control, power control and user selection policies). Finally, we would also like to consider distributive implementation for some cases where the QSI and CSI are only locally available at each nodes in the wireless network. This is important because the centralized solution requires knowledge of the global CSI and global QSI which is very difficult to collect in realtime.

Examples of delay optimal control problems
-
-System Topology: L independent application streams multiplexed on a MIMO link
-
-Derive delay-optimal precoder and power allocation policies
-
-Q1) Should the precoder diagonalize the MIMO channel? - yes!
-
-Q2) What is the structure of power control? - Multilevel water filling
-
-Q3) How to compute the value function of the Bellman’s equation realtime?
[Ref] V.K.N.Lau, Y.Chen, “Delay-Optimal Precoder Design for MultiStream MIMO System”, to appear IEEE Transactions on Wireless Communications, 2009
(A) Delay-Optimal MIMO precoder design for multi-stream MIMO Systems
-
-System Topology: Multi-user MIMO Systems with K users doing SDMA
-
-Derive delay-optimal user selection, precoder and power allocation policies
-
-Q1) How to have low complexity user selection scheme for delay-optimal SDMA
-
-Q2) What is the structure of power control? - Multilevel water filling
-
-Q3) How to overcome the curse of dimensionality
-
-Q4) Any insight on Buffer Size Requirement, SNR, Packet Drop Rate and number of users in the system?
[Ref] S. Ruan, V.K.N. Lau, “Delay Sensitive Precoding Design for Multi-user SDMA using Stochastic Decomposition”, IEEE Transactions on Wireless Communications, 2008 (submitted)
(B) Delay-Optimal User Selection and power control for Multi-user MIMO with Limited buffer size

-
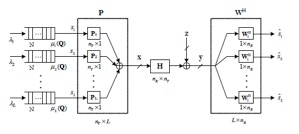
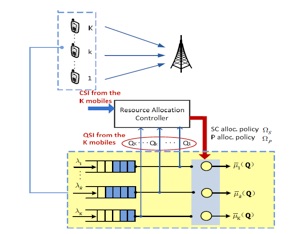
-System Topology: Multi-user OFDMA Systems with K users and N subbands
-
-Derive delay-optimal user selection and power allocation policies
-
-Q1) How to have low complexity control policy for delay-optimal OFDMA?
-
-Q2) What is the structure of power control and user selection? - Multilevel water filling
-
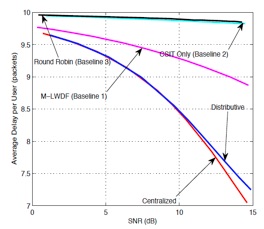
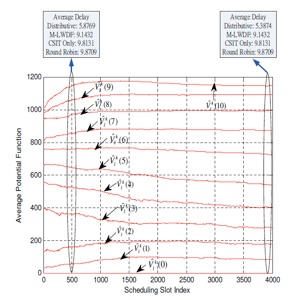
-Q3) How to overcome the curse of dimensionality? - Distributive stochastic learning, simultaneous update of Lagrange Multipliers and Potential Functions
-
-Q4) Distributive Implementation? - Approximate MDP and Per-node Potential function
-
-Q5) Convergence Analysis? - Updates in the same time scale as CSI and QSI (no need to converge within a coherence time); Almost sure convergence; Asymptotic Global Optimal Performance.
[Ref] V.K.N.Lau, Y. Cui, “Delay Optimal Power and Subcarrier Allocation for OFDMA System via Stochastic Approximation”, IEEE Transactions on Wireless Communication, 2008 (submitted)
(C) Delay-Optimal Cross-Layer Control for OFDMA Systems

-
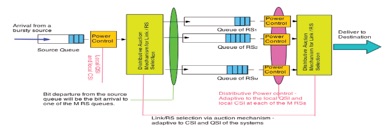
-System Topology: two hop cooperative wireless system with a source node, M relay nodes and a destination node.
-
-Derive delay-optimal relay selection and power allocation policies
-
-Q1) How to overcome the complex interactions of queues in the system?
-
-Q2) What is the structure of power control and relay selection?
-
-Q3) How to overcome the curse of dimensionality? - Distributive stochastic learning, simultaneous update of Lagrange Multipliers and Potential Functions
-
-Q4) Distributive Control (function of local CSI and local QSI only)?
-
-Q5) Convergence Analysis? Under what conditions will the online algorithm converge?
-
-Q6) What is the asymptotic performance of the distributive solution?
[Ref] R. Wang, V.K.N.Lau, “Delay Optimal Two-Hop Cooperative Communications via Approximate MDP and Distributive Online Stochastic Learning”, IEEE Transactions on Information Theory, 2009 (submitted).
(D) Delay-Optimal Cross-Layer Control for Two-hop Cooperative Communications - Approximate MDP and Distributive stochastic Learning